Sự tăng lên của các bước và không gian nguồn lực tính toán theo thời gian.

Ở các ví dụ trước minh chứng cho việc các tiến trình có thể tiêu tốn một tỉ lệ nguồn lực để tính toán khác nhau. Một cách hay để diễn tả sự khác biệt này là sử dụng khái niệm sự tăng lên của các bược và không gian nguồn lực tính toán theo thời gian(order of growth). Một sự đo lường nguồn lực tính toán được yêu cầu bởi tiến trình khi giá trị input càng lớn.

Với n là một biến nhập vào đo lường kích thước của vấn đề, và R(n) số nguồn lực máy tính tiến trình yêu cầu để giải quyết vấn đề trong với kích thước n. Trong các ví dụ trước chúng ta đã lấy giá trị n là một số yêu cầu được tính toán của một function cho trước, nhưng có thể trong các trường hợp khác cũng thế.

Ví dụ, nếu chúng ta muốn tính xắp xỉ căn bậc hai của một số, chúng ta xem n trở thành một số input đầu vào. Với phép nhân tăng lên theo số dòng n để thực hiện. Tương tự, R(n) đo lường số register lưu trữ nội bộ được sử dụng, số lượng nguồn lực để trình diễn việc tính toán. Trong máy tính, số lượng các hoạt động tính toán là cố định ở một thời điểm nào đấy, thời gian yêu cầu sẽ tỉ lệ tương xứng với số lượng các tính toán thiết bị cơ bản được trình diễn.

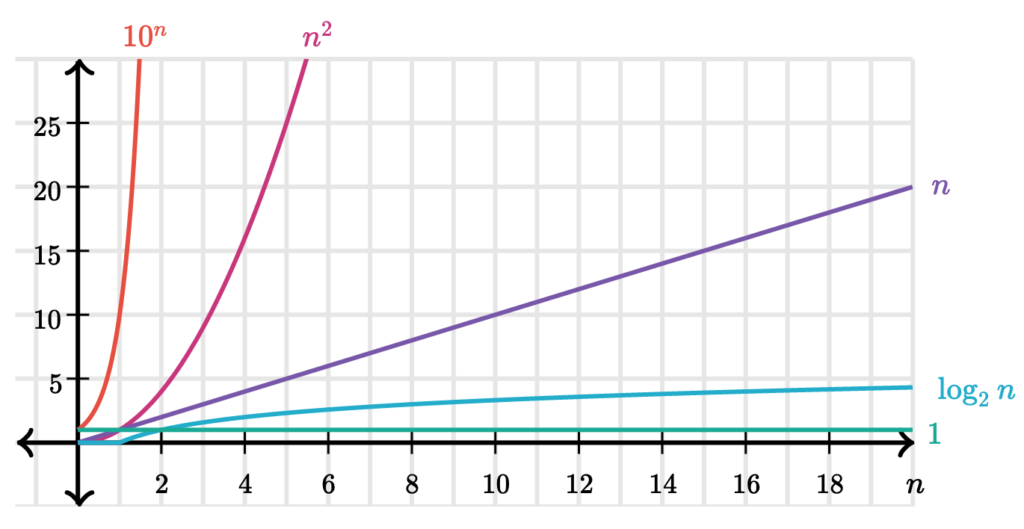
Chúng ta có thể kết luận rằng R(n) có (order of growth) Θ(f (n)), được viết là R(n) = Θ(f (n)) ( được gọi là “theta của f(n)”, nếu có hai hằng số dương độc lập k1 và k2 với n như rằng k1 f (n) ≤ R(n) ≤ k2 f (n) cho bất kì giá trị lớn nào của n.( Có nghĩa là, với n càng lớn, nhưng giá trị của R(n) vẫn chỉ dịch chuyển trog khoảng k1 f (n) and k2 f (n)).

Ví dụ thực tế: với tiến trình đệ quy tiến tính cho việc tính Factorial trong bài (Tính giai thừa của một số). Số lượng bước yêu cầu tăng tương ứng với giá trị của input n. Hơn nữa, số bước yêu cầu cho tiến trình này cũng tăng như Θ(n). Không gian tính toán cần thiết cũng tăng tuyến tính như là Θ(n).

Đối với tiến trình tính giai thừa của n sử dụng vòng lặp, số lượng bước yêu cầu cũng là Θ(n), nhưng không gian tính toán chỉ là Θ(1) – là một hằng số cố định. Việc tính số Fib sử dụng cây đệ quy trong bài (Cây đệ quy) yêu cầu Θ(ϕ^n) bước thực hiện và không gian tính toan là Θ(n), ϕ là một tỉ lệ vàng (1.6180)

Mặt khác, order of growth mang lại một chỉ số hữu ích về cách chúng ta có thể mong chờ sự thay đổi hành vi của quá trình khi chúng ta thay đổi kích thước vấn đề. Đối với quy trình Θ(n) (tuyến tính như đệ quy tuyến tính), việc tăng gấp đôi kích thước sẽ tăng gấp đôi lượng không gian nguồn lực cần sử dụng. Đối với một tiến trình tính lũy thừa, mỗi lần tăng kích thước bài toán sẽ cần nhân lên
việc sử dụng không gian tài nguyên tính toán theo hệ số không đổi. Chúng ta sẽ tìm hiểu vấn đề này ở bài tiếp theo. Exponentiation