Đề xuất rằng chúng ta muốn làm các phép toán đại số với các phân số. Chúng ta có thể thực hiện các phép toán cộng, trừ , nhân và chia cho hai phân số và kiểm tra xem liệu rằng hai phân số có bằng nhau không?
Phép toán hai phân số
Cho rằng chúng ta đã định nghĩa việc khởi tạo phân số từ tử số và mẫu số. Cũng như có cách để lấy tử số và mẫu số từ một phân số cho trước. Việc thực hiện khởi tạo và lấy giá trị đã được định nghĩa như là các procedure.
- (make-rat ⟨n⟩ ⟨d ⟩) trả về một phân số có tử là n và mẫu là d (n và d là các số integer)
- (numer ⟨x⟩) trả về tử số của phân số x
- (denom ⟨x⟩) trả về mẫu số của phân số x
Đây là các procedure giả sử chúng ta cần để có một phân số hoàn chỉnh. Chúng ta vẫn chưa nói về cách trình bày một phân số, hoặc các procedure numer, demon và make-rat sẽ thực thi như thế nào. Thậm chí nếu chúng ta đã trình bay các procedure đó, chúng ta có thể công, trừ, nhân , chia hai phân số, và kiểm tra xem chúng có bằng nhau không sử dụng công thức bên dưới:
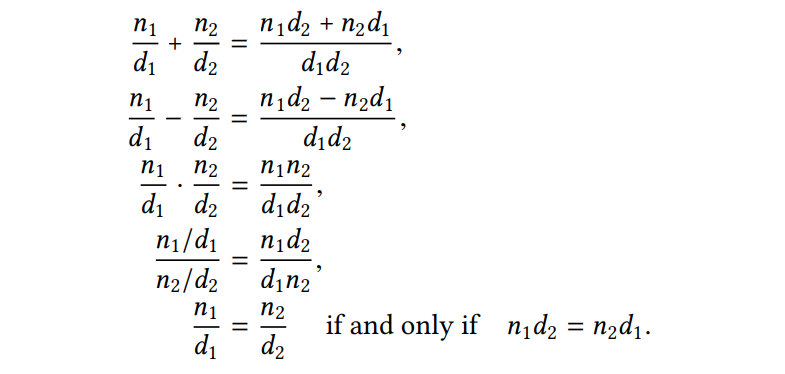
Chúng ta có thể biểu diễn các công thức trên bằng các procedure như sau”:
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
(define (equal-rat? x y)
(= (* (numer x) (denom y))
(* (numer y) (denom x))))Giờ đây, chúng ta đã có các toán tử của các phân số được định nghĩa nghĩa dựa trên các procedure numer, denom, and make-rat. Nhưng chúng ta vẫn chưa định nghĩa chúng là cái gì. Chúng ta cần một cách để kết dính tử số và mẫu số để hình thành một phân số.
Pairs
Để thuận tiện cho việc triển khai mức độ data abstraction cụ thể, ngôn ngữ cung cấp một cấu trúc phức hợp được gọi là pair – cặp, được khởi tạo với thủ tục sơ khai cons . Procedure cons cần hai đối số và trả về data object phức hợp bao gồm hai đố số trên. Với một pair ban đầu, chúng ta có thể truy xuất các phần của nó sử dụng các procedure nguyên thủy là car và cdr. Sử dụng cons, car và cdr như sau.
(define x (cons 1 2))
(car x)
1
(cdr x)
2Pair là một kiểu dữ liệu được gán một cái tên và sử dụng nó, cũng giống như các đối tượng dữ liệu nguyên thủy. Hơn nữa, cons được sử dụng để tạo thành các pairs và cách thành phần của nó là các pair con, và hơn thế nữa:
(define x (cons 1 2))
(define y (cons 3 4))
(define z (cons x y))
(car (car z))
1
(car (cdr z))
3Các data object được khởi tạo từ pair được gọi là danh sách dữ liệu có cấu trúc.
Trình bày các phân số
Pair cung cấp một cách tự nhiên để hoàn thiện mối quan hệ của phân số. Đơn giản để trình bày một phân số ta chỉ cần trình bày pair của hai số integer: tử số và mẫu số. Khi đó các procedure make-rat, numer, và denom được trình bày như sau:
define (make-rat n d) (cons n d))
(define (numer x) (car x))
(define (denom x) (cdr x))Và để hiển thị kết quả tính toán phân số, chúng ta có thể in ra các phân số bằng việc in tử số, dấu ‘/’ và mẫu số như sau:
(define (print-rat x)
(newline)
(display (numer x))
(display "/")
(display (denom x)))Giờ hãy xem thử các procedure phân số thực thi xem sao
(define one-half (make-rat 1 2))
(print-rat one-half)
1/2
(define one-third (make-rat 1 3))
(print-rat (add-rat one-half one-third))
5/6
(print-rat (mul-rat one-half one-third))
1/6
(print-rat (add-rat one-third one-third))
6/9Bạn cũng có thể thấy kết quả cuối cùng, thực thị phân số không giảm giá trị của tử số và mẫu số đến số nhỏ nhât. Vì thế ta có thể làm điều này bằng cách thay đổi đôi chút procedure make-rat.
(define (make-rat n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))gcd là procedure tìm ước chung lớn nhất của hai số integer. Sau đó ta sẽ chia tử và mẫu số cho ước chung lớn nhất. Giờ chúng ta có kết quả hoàn chỉnh
(print-rat (add-rat one-third one-third))
2/3
Việc sửa đổi đạt được bằng việc thay đổi procedure make-rat mà không cần thay đổi bất kì thủ tục nào khác ( như là add-rat và mul-rat) .
Bài viết tiếp theo: Abstraction Barriers




One thought on “Ví dụ: Các toán tử đại số cho các phân số.”