Một cách để nhìn nhận data abstraction như là một ứng dụng của “nguyên tắc ít cam kết”. Trong việc thực thi số phức, chúng ta có thể sử dụng cách trình bày của Ben hoặc Alyssa. Ranh giới của abstraction được định hình bởi selectors và constructors cho phép chúng ta trì hoãn việc chọn việc trình bày số phức ở mức lâu nhất có thể cho dữ liệu và duy trì tính linh hoạt trong việc thiết kế hệ thống.
Nguyên lý ít cam kết co thể được tiến hành có thể được thực hiện cực kỳ hiệu quả. Nếu muốn, chúng ta có thể duy trì sự mơ hồ trong việc biễu diễn số phức thậm chí sau khi chúng ta đã thiết kế selectors và constructors, và đồng thời sử dụng cách của Ben và Alyss. Nếu cả hai đều bao gồm trong một hệ thống đơn, chúng ta sẽ cần một vài cách để phân biệt dữ liệu trong “polar form” và dư liệu trong “retangular form”. Mặt khác, nếu chúng ta muốn tìm magnitude của (3, 4), chúng ta sẽ không biết liệu rằng câu trả lời là 5 ( retangular form) hoặc 3 ( polar form). Cách đơn giản đễ đạt được sự khác biệt này là sử dụng loại “tag” – biểu tượng cho retangular hoặc polar – như là một phần của số phức . Khi chúng ta thao tác với một số phức, chúng ta có thể sử dụng tag để quyết định procedure selector nào được áp dụng.
Để thao tác với “tag”, chúng ta cho rằng có một procedure “type-tag” và nội dụng của nó là truy xuất data object “tag” và nội dung thực (các tọa độ của polar hoặc retangular, trong trường hợp của một số phức). Chúng ta cũng đề xuất một procedure attach-tag nó cần một “tag” và “content” và tạo ra một data object đã được tag. Một cách dễ dàng để thực thi là sử dụng cấu trúc list.
(define (attach-tag type-tag contents)
(cons type-tag contents))
(define (type-tag datum)
(if (pair? datum)
(car datum)
(error "Bad tagged datum: TYPE-TAG" datum)))
(define (contents datum)
(if (pair? datum)
(cdr datum)
(error "Bad tagged datum: CONTENTS" datum)))Sử dụng các procedure này, chúng ta có thể định nghĩa việc dự đoán retangular? và polar?,
(define (rectangular? z)
(eq? (type-tag z) 'rectangular))
(define (polar? z) (eq? (type-tag z) 'polar))Với loại tag, Ben và Alyssa có thể sửa đổi code của họ để cùng tồn tại trong hệ thống. Bất cứ khi nào Ben khởi tạo một số phức, anh ta sử dụng tag “retangular”. Và Alyssa sử dụng tag “polar”. Hơn nữa, Ben và Alyssa phải chắc rằng tên các procedure không bị nhầm lẫn. Một cách để làm điều này là Bend thêm tiền tố “retangular” vào tên mỗi các procedure trình bày của anh ta và Alyssa thêm “polar” vào. Đây là cách trình bày sửa đổi retangular của Ben ở bài trước.
(define (real-part-rectangular z) (car z))
(define (imag-part-rectangular z) (cdr z))
(define (magnitude-rectangular z)
(sqrt (+ (square (real-part-rectangular z))
(square (imag-part-rectangular z)))))
(define (angle-rectangular z)
(atan (imag-part-rectangular z)
(real-part-rectangular z)))
(define (make-from-real-imag-rectangular x y)
(attach-tag 'rectangular (cons x y)))
(define (make-from-mag-ang-rectangular r a)
(attach-tag 'rectangular
(cons (* r (cos a)) (* r (sin a)))))Và đây là cách trình bày polar đã được sửa đổi
(define (real-part-polar z)
(* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z)
(* (magnitude-polar z) (sin (angle-polar z))))
(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (make-from-real-imag-polar x y)
(attach-tag 'polar
(cons (sqrt (+ (square x) (square y)))
(atan y x))))
(define (make-from-mag-ang-polar r a)
(attach-tag 'polar (cons r a)))Mỗi selector được thực thi như là một procedure để kiểm tra tag của đối số của nó và gọi procedure tương ứng cho việc xử lý data. Ví dụ, để đạt được phần real của một số phức, real-part tag quyết định liệu rằng sử dụng real-part retangualr hoặc real-part polar.
(define (real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
(else (error "Unknown type: REAL-PART" z))))
(define (imag-part z)
(cond ((rectangular? z)
(imag-part-rectangular (contents z)))
((polar? z)
(imag-part-polar (contents z)))
(else (error "Unknown type: IMAG-PART" z))))
(define (magnitude z)
(cond ((rectangular? z)
(magnitude-rectangular (contents z)))
((polar? z)
(magnitude-polar (contents z)))
(else (error "Unknown type: MAGNITUDE" z))))
(define (angle z)
(cond ((rectangular? z)
(angle-rectangular (contents z)))
((polar? z)
(angle-polar (contents z)))
(else (error "Unknown type: ANGLE" z))))Để thực thi các phép toán đại số với số phức, chúng ta có thể sử dụng các procedure add-complex, sub-complex, mul-complex, và div-complex ở bài viết trước. Vì selector là chung cho các cách trình bày số phức, nên cũng sẽ hoạt động tương tự cho hai cách trình bày. Ví dụ, procedure add-complex vân là
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))Cuối cùng, chúng ta phải chon cách khởi tạo số phức sử dụng cách của Ben hoặc Alyssa. Một sự lựa chọn hợp lý là construct số phức từ retangular form khi có real và imaginary và construct số phức từ polar form khi có magnitudes và angles.
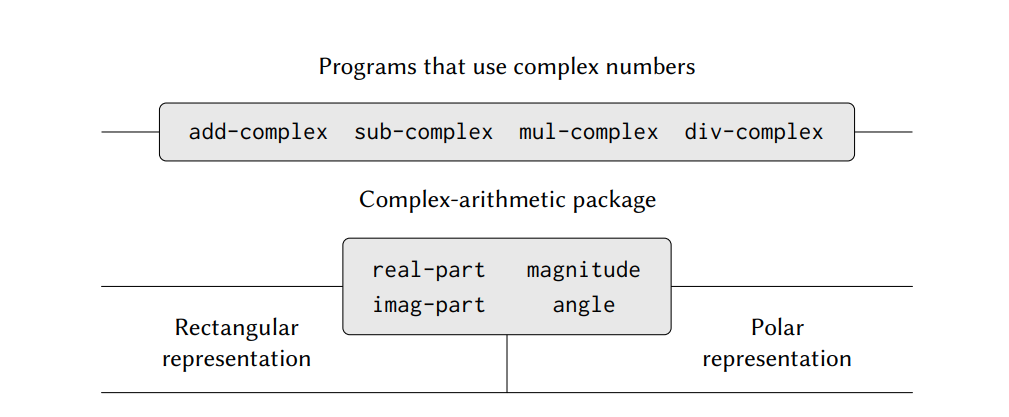
(define (make-from-real-imag x y)
(make-from-real-imag-rectangular x y))
(define (make-from-mag-ang r a)
(make-from-mag-ang-polar r a))Kết quả của hệ thống số phức được phát thảo trong hình 2.21. Hệ thống tách biệt thành 3 phần độc lập nhau: các phép toán đại số của số phức, trình bày số phức của Ben và Alyssa. Việc thực thi kiểu polar và retangular có thể được phát triểu bởi Ben và Alyssa hoạt động riêng biệt, và cả hai cũng được sử dụng để trình bày cơ sở bởi một trình viên thứ ba thực thi các procedure đại số của số phức trong các điều khoản của constructor/selector.



