Các procedure như là các argument truyền vào procedure khác.

Hãy cùng nhau phân tích 3 procedure sau;

Procedure đầu tiên tính tổng của các số nguyên từ a đến b.

(define (sum-integers a b)
(if (> a b)
0
(+ a (sum-integers (+ a 1) b))))

Procedure thứ hai là tính tổng của của các lập phương của các số nguyên trong khoảng cho trước

(define (sum-cubes a b)
(if (> a b)
0
(+ (cube a)
(sum-cubes (+ a 1) b))))

Thứ ba là tỉnh tổng của môt dãy các điều kiện của chuỗi điều khoản:

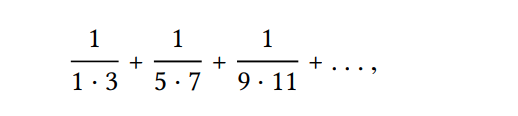
Kết quả tính toán bao hàm đến giá trị của π/8

(define (pi-sum a b)
(if (> a b)
0
(+ (/ 1.0 (* a (+ a 2)))
(pi-sum (+ a 4) b))))

Ba procedure này rõ ràng chia sẽ cùng một công thức tính toán mô hình chung. Chúng hầu hết đều giống hệt nhau, chỉ khác nhau ở tên của procedure, chức năng của a được sử dụng để tính toán số hạng được thêm vào và hàm cung cấp giá trị tiếp theo của a. Chúng ta có thể tạo ra các thủ tục trên bằng cách điền vào các ô trống trong cùng một mẫu bên dưới:

(define (⟨name⟩ a b)
(if (> a b)
0
(+ (⟨term⟩ a)
(⟨name⟩ (⟨next⟩ a) b))))

Việc trình bày một mô hình chung như trên là bằng chứng thuyết phục cho thấy luôn có một sự trừu tượng chung hữu ích đang chờ được khám phá ra cho các thuật toán chung. Thật vậy, các nhà toán học từ lâu đã xác định được tính trừu tượng của phép tính tổng của một chuỗi và đã phát minh ra “ký hiệu sigma”, chẳng hạn để khái quát hóa khái niệm này.

Lợi ích to lớn mà ký hiệu sigma mang lại là nó cho phép các nhà toán học xử lý chính khái niệm tính tổng thay vì chỉ với các tổng cụ thể—ví dụ, công thức hóa các kết quả tổng quát về các tổng độc lập với chuỗi cụ thể được tính tổng.

Tương tự, với tư cách là người thiết kế chương trình, chúng ta muốn ngôn ngữ đủ mạnh để có thể viết một thủ tục thể hiện khái niệm tính tổng thay vì chỉ các thủ tục tính các tổng cụ thể. Chúng ta có thể làm điều đó một cách dễ dàng bằng ngôn ngữ thủ tục bằng cách lấy mô hình chung được hiển thị ở trên và chuyển đổi các “chỗ muốn thay thế” thành các tham số mong muốn:

(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))

Lưu ý rằng procedure sum lấy các arguments là giới hạn dưới và giới hạn trên a
và b cùng với term, next. Chúng ta có thể sử dụng procedure sum giống như bất kỳ thủ tục nào. Ví dụ: chúng ta có thể sử dụng nó (cùng với thủ tục inc tăng đối số của nó lên 1) để xác định sum-cubes:

(define (inc n) (+ n 1))
(define (sum-cubes a b)
(sum cube a inc b))

Sử dụng thủ tục sum-cubes, chúng ta có thể tính tổng của các cube của các số nguyên từ 1 đến 10:

(sum-cubes 1 10)
3025

Cùng với sự hỗ trợ của thủ tục identity để tính term, chúng ta có thể đĩnh nghĩa sum-integer trong các term của sum.

(define (identity x) x)
(define (sum-integers a b)
(sum identity a inc b))

Sau đó có thể sử dụng để tính tổng các số nguyên từ 1 đến 10 như sau:

(sum-integers 1 10)
55

Chúng ta cũng có thể định nghĩa pi-sum như sau:

(define (pi-sum a b)
(define (pi-term x)
(/ 1.0 (* x (+ x 2))))
(define (pi-next x)
(+ x 4))
(sum pi-term a pi-next b))

Sử dụng procedure này , chúng ta có thể tính xấp xỉ giá trị của π:

(* 8 (pi-sum 1 1000))
3.139592655589783

Sau khi có công thức tính sum, chúng ta có thể sử dụng nó như là các building block trong việc công thức hóa nhiều hơn các khái niệm khác. Ví dụ, tích phân của hàm f giữa các giới hạn a và b có thể được tính gần đúng bằng số dưới công thức:

Với các giá trị nhỏ của dx. Chúng ta có thể trình bày tích phân trên như là một procedure.

(define (integral f a b dx)
(define (add-dx x)
(+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b)
dx))

(integral cube 0 1 0.01)
.24998750000000042
(integral cube 0 1 0.001)
.249999875000001

( Gía trị chính xác của tích phân cube giữa 0 và 1 là 1/4)

Bài viết tiếp theo: Constructing Procedures Using lambda