Chúng ta đã làm quen với các thủ tục bao hàm như một cơ chế trừu tượng hóa các mô hình của các phép toán số học để làm cho chúng độc lập với các số cụ thể có liên quan. Với các thủ tục bậc cao hơn, chẳng hạn như thủ tục tích phân trong bài các thủ tục như là argument, chúng ta bắt đầu thấy được một loại trừu tượng mạnh mẽ hơn: các thủ tục được sử dụng để thể hiện các phương pháp tính toán chung, độc lập với các hàm cụ thể có liên quan.

Trong bài này chúng ta thảo luận về hai ví dụ phức tạp hơn—các phương pháp chung để biến số x khi f(x) = 0 và điểm cố định của hàm số f(x) = x —và chỉ ra cách các phương pháp này có thể được biểu diễn trực tiếp dưới dạng thủ tục.
Tìm nghiệm x của phương trình bằng phương pháp nữa khoảng
Phương pháp nữa khoảng tuy đơn giản nhưng là một kĩ thuật hữu ích để tìm nghiệm của phương trình f(x) = 0, nơi f là một hàm liên tục. Ý tưởng nêu rằng, nếu chúng ta có các điểm a và b sao cho f(a) < 0 < f(b) , thì f phải có ít nhất số 0 giữa a và b. Để xác định số 0, gọi x là trung bình của a và b, rồi tính f(x). Nếu f(x) > 0 thì f phải có số 0 nằm giữa a và x. Nếu f(x) < 0 thì f phải có số 0 nằm giữa x và b.
Tiếp tục theo cách này, chúng ta có thể nhận ra các khoảng ngày càng nhỏ dần mà trên đó f phải có số 0. Khi chúng tôi đạt đến một điểm mà khoảng cách đủ nhỏ thì quá trình dừng lại. Khi đó khoảng giảm đi một nửa ở mỗi bước của tiến trình, số bước cần thiết tăng lên là Θ(log(L/T )), trong đó L là độ dài của khoảng ban đầu và T là sai số chấp nhận (nghĩa là kích thước của một khoảng chúng ta sẽ coi là “đủ nhỏ”). Đây là một procedure để thực hiện tiến trình này:
(define (search f neg-point pos-point)
(let ((midpoint (average neg-point pos-point)))
(if (close-enough? neg-point pos-point)
midpoint
(let ((test-value (f midpoint)))
(cond ((positive? test-value)
(search f neg-point midpoint))
((negative? test-value)
(search f midpoint pos-point))
(else midpoint))))))Chúng ta giả sử rằng ban đầu chúng ta có hàm f cùng với những điểm tại đó giá trị của nó là âm và dương. Đầu tiên chúng ta tính trung điểm của hai điểm đã cho. Tiếp theo, chúng tôi kiểm tra xem khoảng đã cho có đủ nhỏ hay không và nếu có thì chúng tôi chỉ cần trả về midpoint làm đáp án. Ngược lại, chúng ta tính giá trị của f tại điểm giữa làm giá trị kiểm tra. Nếu giá trị kiểm tra là dương thì chúng ta tiếp tục quá trình với một khoảng mới chạy từ điểm âm ban đầu đến điểm giữa. Nếu giá trị kiểm tra là âm, chúng ta tiếp tục với khoảng từ điểm giữa đến điểm dương. Cuối cùng, có khả năng giá trị kiểm tra là 0, trong trường hợp đó midpoint là đáp án mà chúng ta đang tìm kiếm,vì
Để kiểm tra xem các endpoint là những số gần đúng chúng ta có thể sủ dụng thủ tục như sau:
(define (close-enough? x y) (< (abs (- x y)) 0.001))
Việc sử dụng search procedure rất khó sử dụng trực tiếp, vì chúng ta có thể vô tình cho nó những điểm mà tại đó các giá trị của f không có các dấu hiệu mong đợi, trong trường hợp đó chúng ta sẽ nhận được kết quả sai. Thay vào đó, chúng ta sẽ sử dụng search thông qua quy trình sau, kiểm tra xem điểm cuối nào làm cho f có giá trị âm và điểm cuối nào có giá trị dương, đồng thời gọi search procedure tương ứng. Nếu hàm có cùng dấu hiệu nhận biết tại hai điểm đã cho thì không thể sử dụng phương pháp nửa khoảng (half-interval method), trong trường hợp đó quy trình báo hiệu lỗi.
(define (half-interval-method f a b)
(let ((a-value (f a))
(b-value (f b)))
(cond ((and (negative? a-value) (positive? b-value))
(search f a b))
((and (negative? b-value) (positive? a-value))
(search f b a))
(else
(error "Values are not of opposite sign" a b)))))Ví dụ sử dụng phương pháp half-interval để tính xấp xỉ giá trị π giữa 2 và 4 của sin x = 0 như sau:
(half-interval-method sin 2.0 4.0)
3.14111328125Đây là một ví dụ khác về việc sử dụng phương pháp nữa khoảng để tìm kiếm giá trị của x cho phương trình x^3 – 2x – 3 = 0 trong khoảng 1 và 2
(half-interval-method (lambda (x) (- (* x x x) (* 2 x) 3))1.0 2.0)
1.89306640625Tìm các điểm cố định của các hàm
Một số x được gọi là điểm cố định (fixed point) của một hàm f nếu x thỏa mãn hằng đẳng thức f(x) = x. Đối với một vài hàm f, chúng ta có thể đoán xem một điểm cố định guess và tính toán hàm f lặp lại liên tục.
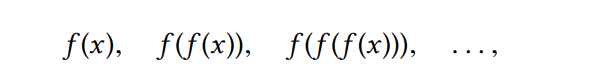
Cho đến khi giá trị không thay đổi nhiều. Sử dụng ý tưởng này, chúng ta có thể nghĩ ra một thủ tục fix-point lấy đầu vào là một hàm và khởi tạo guess và đưa ra giá trị gần đúng cho một điểm cố định của hàm. Chúng ta áp dụng hàm này nhiều lần cho đến khi tìm thấy hai giá trị liên tiếp có hiệu nhỏ hơn một số nhỏ không đáng kể:
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2))
tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))Ví dụ chúng ta sử dụng phương pháp này để tìm điểm cố định cho hàm cosine, bắt đầu với giá trị 1:
(fixed-point cos 1.0)
.7390822985224023(fixed-point (lambda (y) (+ (sin y) (cos y)))
1.0)
1.2587315962971173
Tiến trình fixed-point gợi lại cho chúng ta tiến trình đã sử dụng để tìm căn bậc hai của một số. Cả hai đều sử dụng ý tưởng lặp lại để cải thiện guess cho đến khi kết quả thỏa mãn một vài tiêu chí. Sự thật, chúng ta cũng có thể tối ưu hóa công thức tìm căn bậc hai như là một thủ tục search điểm cố định. Việc tìm căn bậc hai của một số x yêu cầu tìm một số y thỏa mãn y^2 = x hoặc có thể suy ra rằng y = x/y, chúng ta nhận thấy rằng việc tìm kiếm điểm cố định của một hàm y thỏa mãn y->x/y , chúng ta try to tính căn bậc hai của x như sau:
(define (sqrt x)
(fixed-point (lambda (y) (/ x y))
1.0))Tiếc là thủ tục search fixed-point này không hội tụ đủ yếu tố cần thiết để tính căn bậc hai. Xem xét guess là y1. Guess tiếp theo là y2 = x/y1 and guess y3 = x/y2 = x/(x/y1) = y1. Các kết quả trong vòng lặp vô tận trong guess y1 và y2 được lặp lại vô số lần, dao động quanh câu trả lời đó.
Một cách để kiểm soát giao đông để ngăn guess thay đổi quá nhiều. Từ đó đáp án luôn ở giữa guess y và x/y, chúng ta có thể đoán một guess mới không quá thay đổi nhiều so với y như x/y bằng cách tính trung bình y và x/y. Từ đó guess tiếp theo sau y là 1/2(y+x/y) thay vì x/y. Tiến trình tạo ra một chuỗi guess đơn giản như là một tiến trình tìm kiếm một fixed-point của y–> 1/2(y+x/y)
(define (sqrt x)
(fixed-point (lambda (y) (average y (/ x y)))
1.0))Chú ý rằng, y = 1/2(y+x/y) đơn giản chỉ là việc chuyển từ biểu thức y = x/y, tích lũy nó, băng cách thêm y đến cả hai vế của biểu thức và và chia hai về cho 2.
Với sửa đổi này, quy trình tính căn bậc hai sẽ hoạt động tốt. Trên thực tế, nếu muốn làm sáng tỏ các định nghĩa, chúng ta có thể thấy rằng chuỗi các phép tính gần đúng với căn bậc hai được tạo ra ở đây hoàn toàn giống với chuỗi được tạo ra bởi thủ tục căn bậc hai ban đầu của chúng ta. Cách tiếp cận này lấy trung bình các xấp xỉ liên tiếp cho một thử nghiệm, một kỹ thuật mà chúng ta gọi là giảm trung bình, thường hỗ trợ sự hội tụ của việc tìm kiếm điểm cố định.
Bài tiếp theo: Procedures as Returned Values




One thought on “Các procedure như là các phương thức chung”