Các ví dụ trước chứng minh cách sử dụng các procedure như là các argument nhằm tăng cường đáng kể cách trình bày ấn tượng của bất kỳ ngôn ngữ lập trình mạnh mẽ. Chúng ta cũng có thể đạt được nhiều ấn tượng hơn bằng cách tạo ra các procedure có giá trị trả về là các procedure.

Procedure avarage-damp
Hãy xem lại ví dụ về fixed-point ở bài trước. Việc công thức hóa một bảng nâng cấp mới của thủ tục tính căn bậc hai sử dụng search fixed-point., tuân thủ như là √x là một fixed-point của hàm y–>x/y. Sau đó chúng ta đã biến đổi công thức để sử dụng giảm trung bình cộng đến xắp xị để bao hàm heets các trường hợp. Một function f cho trước, chúng ta có thể xem giá trị của f ở x là trung bình của x và f(x).
Trình bày ý tưởng giảm trung bình được thể hiện qua procdure sau:
(define (average-damp f)
(lambda (x) (average x (f x))))Procedure average-damp lấy f là một argument và trả về giá trị một procedure( sử dụng lambda – hàm vô danh), khi áp dụng cho một số x, procedure sư dụng lambda tính giá trị trụng bình của x và f(x). Ví dụ, sử dụng average-damp đến thủ tục tính bình phương tạo ra giá trị của x là trung bình của x và x^2. Áp dụng với x là 10 sẽ trả về giá trị trung bình của 10 và 100 là 55.
((average-damp square) 10)
55
Sử dụng avergae-damp, chúng ta có thể công thức hóa lại của thủ tục square-root như sau:
(define (sqrt x)
(fixed-point (average-damp (lambda (y) (/ x y)))
1.0))Công thức trên làm minh bạch ba ý tưởng trong phương thức: fixed-point search, average damping, and the function y→ x/y. Cần so sánh công thức trên với công thức tính gốc tính căn bậc hai ở bài này . Nhớ rằng cả hai procedure đều trình bày cùng tiến trình tính, và ý tưởng sẽ trở nên rõ ràng, rành mạch hơn khi ta trình bày tiến trình trong các điều khoản của các abstraction. Nhìn chung, có nhiều cách để công thức hóa một tiến trình thành một thủ tục. Các lập trình viên chuyên nghiệp biết cách chọn việc công thức hóa thủ tục dễ nhận ra nhất và các thành phần hữu dụng của tiến trình được trình bày dưới dạng các thực thể tách biệt để có thể tái sử dụng lại trong các ứng dụng khác. Ví dụ, như căn bậc ba của x là một fixed-point của hàm y->x/y^2, chúng ta có thể khái quát hóa thủ tục tính căn bậc hai để truy xuất căn bậc ba:
(define (cube-root x)
(fixed-point (average-damp (lambda (y) (/ x (square y))))
1.0))
Phương thức Newton’s
Khi procedure tính căn bậc hai được đưa ra ở bài trước. Có một trường hợp đặt biệt của phương thức Newton’s . Nếu x→ g(x) là một hàm khác, thì một giải pháp của biểu thức g(x) = 0 là một fixed-point của function x->f(x), ở đó
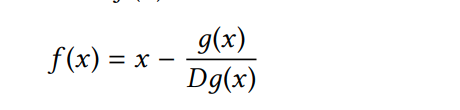
và Dg(x) là đạo hàm của g tính tại x. Phương pháp Newton sử dụng phương pháp điểm cố định mà chúng ta đã thấy ở trên để tính gần đúng nghiệm của phương trình bằng cách tìm fixed-point của hàm f
Đối với nhiều hàm g và để có những guess ban đầu đủ tốt cho x, Phương pháp Newton hội tụ nhiều điểm để đưa ra nghiệm nhanh cho phương trình g(x) = 0.
Để thực thi phương pháp Newton’s như một procedure, đầu tiên ta phải trình bày ý tưởng đạo hàm. Để ý rằng “đạo hàm” giống trung bình giảm dần (average-damping) trước, chuyển từ một function đến một function khác. Ví dụ, đạo hàm của function x->x^3 là X->3x^2. Nói chung, nếu g là một function và dx là số nhỏ, thì đạo hàm của Dg của f la function mà giá trị của nó ở bất kì số x nào được tính như sau:
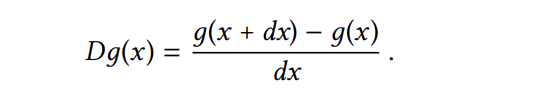
Hơn nữa, chúng ta có thể trình bay ý tưởng đạo hàm như là một procedure.(dx là 0.00001)
(define (deriv g)
(lambda (x) (/ (- (g (+ x dx)) (g x)) dx)))
(define dx 0.00001)Cũng giống như average-damp, deriv là một procedure với một procedure khác là một arguments và trả về một giá trị là một procedure. Ví dụ, tính xắp xỉ đạo hàm của x->x^3 với 5 ( giá trị chính xác là 75) chúng ta có thể đánh giá như sau:
(define (cube x) (* x x x))
((deriv cube) 5)
75.00014999664018Với sự trợ giúp của procedure deriv, phương pháp Newton’s như là một tiến trình fixed-point được trình bày như sau:
(define (newton-transform g)
(lambda (x) (- x (/ (g x) ((deriv g) x)))))
(define (newtons-method g guess)
(fixed-point (newton-transform g) guess))For instance, to find the square root of x, we can use Newton’s method to find
a zero of the function y 7→ y
2 − x starting with an initial guess of 1.
Để tìm căn bậc hai của x, chúng ta có thê sử dụng phương pháp Newton’s để tìm một số 0 của hàm y->y^2 – x: bắt đầu với giá trị guess khởi tạo là 1.
Đây là cách khác để trình bay thủ tục square-root:
(define (sqrt x)
(newtons-method
(lambda (y) (- (square y) x)) 1.0))Tính Trừu tượng và các first-class procedure
Chúng ta đã khám phá ra hai cách để trình bày việc tính căn bậc hai của một số từ công thức chung một là search fixed-point và một sử dụng phương thức Newton’s. Vì phương pháp Newton chính nó là một quá trình tìm fixed-point, nên chúng ta thấy có hai cách để tính căn bậc hai dựa trên fixed-point. Mỗi phương pháp bắt đầu với một hàm và tìm một điểm fixed-point của một số phép biến đổi của hàm. Chúng ta có thể trình bày ý tưởng chung như là một procedure.
(define (fixed-point-of-transform g transform guess)
(fixed-point (transform g) guess))Một procedure với các inputs là một procedure g, tranform và một guess khởi tạo. Gía trị trả về là một điểm fixed-point của procedure được chuyển đổi.
Sử dụng tính trừu tượng này, chúng ta có thể xem xét lại việc tính căn bậc hai đầu tiên trong bài này ( nơi giá trị fixed-point của việc giá giảm trung bình của y->x/y) như là ví dụ của phương thức chung.
(define (sqrt x)
(fixed-point-of-transform
(lambda (y) (/ x y)) average-damp 1.0))Tương tự, việc tính căn bậc hai sử dụng công thức thứ hai (như là ví dụ về phương pháp Newton’s để tìm điểm fixed-point của sự biến đổi y->y^2 -x ) như sau
(define (sqrt x)
(fixed-point-of-transform
(lambda (y) (- (square y) x)) newton-transform 1.0))Bài viết tiếp theo: Building Abstractions with Data



