Chúng ta cùng bắt đầu bài viết bằng vấn đề tính lũy thừa của một số bất kì cho trước n. Tạo một thủ tục để tính lũy thừa nhận các đối số cơ bản là b và một số lũy thừa dương là n, hãy tính b^n. Một cách để tính là định nghĩa một thủ tục đệ quy .

b^n = b · b^(n−1),
b^0 = 1,
Chúng ta có thể định nghĩa một thủ tục để tính lũy thừa như sau
(define (expt b n)
(if (= n 0)
1
(* b (expt b (- n 1)))))
Đây là một tiến trình đệ quy tuyến tính , nó yêu cầu Θ(n) bước và Θ(n) không gian tính toán. Cũng như với tính giai thừa, chúng ta cũng có thể chuyển đổi thành một tiến trình lặp tuyến tính như sau:
(define (expt b n)
(expt-iter b n 1))
(define (expt-iter b counter product)
(if (= counter 0)
product
(expt-iter b
(- counter 1)
(* b product))))
Tiến trình lặp yêu cầu Θ(n) bước và Θ(1) không gian tính toán.
Chúng ta cũng có thể tính toán lũy thừa của một số trong một vài bước sử dụng phép tính bình phương liên tiếp. Ví dụ muốn tính lũy thừa b^8 như sau:
b · (b · (b · (b · (b · (b · (b · b)))))) ,
Chúng ta có thể tính toán b^8 bằng cách sử dụng ba lần nhân liên tiếp như sau
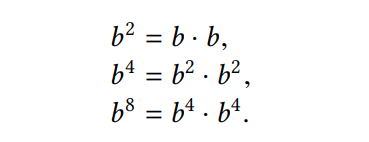
Chúng ta có thể tận dụng sự bình phương liên tiếp này để tính lũy thừa theo nguyên tắc chung khi chúng ta sử dụng nguyên tắc sau:
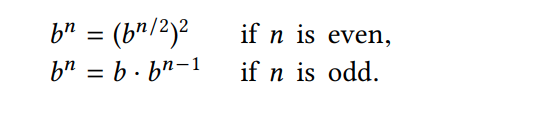
Chúng ta có thể trình bày phương thức trên như là một thủ tục như sau
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1))))))
Với thủ tục kiểm tra một số có phải là số chắc hay không ta:
(define (even? n) (= (remainder n 2) 0))
Tiến trình tính toán lũy thừa với thủ tục là “fast-expt” tăng tuyến tính với log(n) trong cả số bước thực hiện và không gian nguồn lực tính toán. Để minh chứng cho điều này, hãy quan sát việc tính b^(2n) sử dụng thủ tục ( “fast-expt” – đã được định nghĩa ở trên), yêu cầu chỉ nhiều hơn 1 lần tính nhân so với khi tính b^n. Số lượng phép nhân yêu cầu cho việc tính lũy thừa n tăng nhanh tương ứng với log(n) cơ số 2. Tiến trình cần tăng theo Θ(logn).
Sự khác biệt giữa Θ(logn) và Θ(n) là điểm cốt lỗi khi n có giá trị lớn. Ví dụ , tính giai thừa với cớ số n là 1000 thì cần 14 lần phép tính nhân.
Bài viết tiếp theo: Greatest Common Divisors




One thought on “Lũy thừa của một số. Exponentiation”