Trước khi tiếp tục với nhiều hơn các ví dụ về dữ liệu phức hợp và data abstraction, hãy cùng xem xét một vài vấn đề liên quan đến ví dụ phân số. Chúng ta đã định nghĩa các toán tử về điều kiện trong sự khởi tạo make-rat và lấy tử và mẫu. Nhìn chung, ý tưởng cơ bản của data abstraction là xác định mỗi loại đối tượng dữ liệu là danh sách cơ bản các toán tử trong nó sự thao tác của các đối tượng dữ liệu sẽ được biễu diễn, và sử dụng các thao tác đó để xử lý dử liệu.
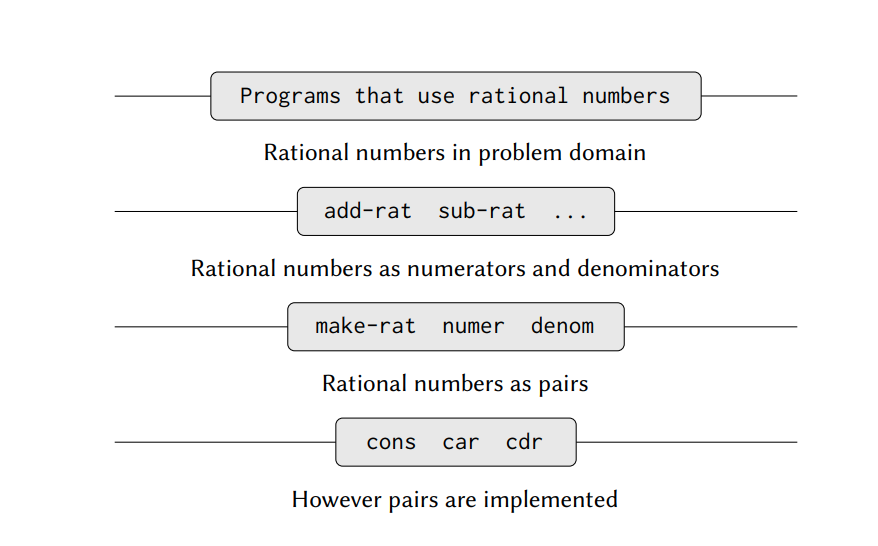
Chúng ta có thể mương tượng cấu trúc của hệ thống phân số như bức hình trên. Các dòng ngang trình bày ranh giới của các abstraction chúng tách biệt hoàn toàn với các mức độ khác nhau của hệ thống. Ở mỗi cấp, ranh giới tách biệt chương trình (ở trên) sử dụng data abstraction từ các chương trình (ở dưới) nó thực thi data abstraction. Các chương trình sử dụng các phân số đê thao tác chúng độc lập trong các điều khoản quy định như: add-rat, sub-rat, mul-rat, div-rat, và equal-rat? Chi tiết cách các pair thực thi không liên quan đến phần còn lại của package phân số miễn là các pair thao tác bằng cách sử dụng cons, car, cdr. Các procedure ở từng cấp là các interface định nghĩa ranh giới của các abstraction và kết nối với các cấp khác nhau.
Phân chia ranh giới có nhiều lợi ích. Một lợi ích xét đến là làm cho chương trình dễ dàng bảo trì và sửa đổi. Bất kì cấu trúc dữ liệu phức tạp nào cũng có thể được biểu diễn từ các cấu trúc dữ liệu nguyên thủy theo nhiều cách khác nhau trong ngôn ngữ lập trình. Việc chọn cách trình bày như thế nào ảnh hưởng đến tính hiệu quả hoạt động của một chương trình. Nếu sự trình bày đó có sự thay đổi nhiều theo thời gian thì tất cả chương trình sẽ phải thay đổi tương ứng. Nhiệm vụ này có lẽ tiêu tốn nhiều thời gian, công sức và chi phí trong các chương trình lớn, sự trình bày ranh giới này độc lập hoàn toàn thành nhiều chương trình module nhỏ hơn.
Ví dụ, một cách thay thế để chỉ ra vấn đề của việc giảm tử số và mẫu số của phân số đến giá trị thấp nhất đến mức không thể chia nữa là biểu diễn việc giảm giá trị bất kể khi nao ta muốn truy xuất các phần của phân số, hơn là khi chúng ta khởi tạo nó. Điều này dẫn đến các procedure khởi tạo và chọn sẽ được thực thi lại như sau
(define (make-rat n d) (cons n d))
(define (numer x)
(let ((g (gcd (car x) (cdr x))))
(/ (car x) g)))
(define (denom x)
(let ((g (gcd (car x) (cdr x))))
(/ (cdr x) g)))Sự khác biệt giữa việc thực thi này với trước đó là một điều sai lầm khi tính gcd (ước chung lớn nhất). Nếu trong việc sử dụng các phân số, chúng ta muốn truy xuất các tử và mẫu của cùng phân số đó nhiều lần, sẽ thích hợp hơn tính toán gcd khi các phân số được khởi tạo . Nếu không, có lẽ sẽ tốt hơn để chờ cho đến khi thời gian truy xuất để tính toán gcd. Trong bất kì trường hợp nào, khi chúng ta thay đổi từ một dạng trình bày này đến dạng khác, các procedure add-rat, sub-rat, … không phải sửa đổi ở tất cả.
Bài viết tiếp theo: What Is Meant by Data?



