Chúng ta sẽ phát triển một hệ thống trình diễn các toán tử đại số trên các số phức như là một ví dụ đơn giản nhưng không phải là một ví dụ thực thế cho một chương trình mà bạn có thể sử dụng các toán tử chung. Chúng ta bắt đầu thảo luận hai cách trình bày các số phức hợp lý như là các pair đã được sắp xếp: retangular form (real part và imaginary part) và polar form ( magnitude và angle). Trong bài này sẽ đưa ra cách trình bày có thể cùng tồn tại trên một hệ thống odwn thông qua việc sử dụng loại “tag” và các toán tử chung.
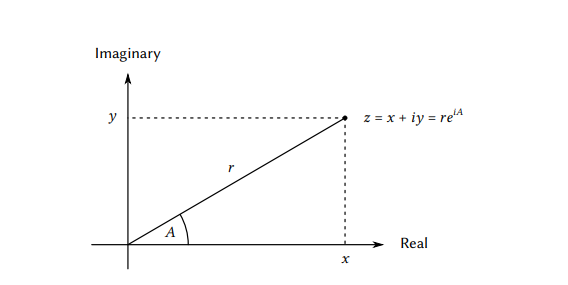
Giống như là các phân số, các số phức cũng được trình bày trong các pair. Một set các số phức có thể được nghĩ như là không gian hai chiều với hai trục vuông góc, trục “real” và trục “imaginary” (Hình 2.2). Từ quan điểm này, số phức là z =x+iy ( i^2 = -1) có thể được xem như là một điểm trên tọa độ nơi tọa độ real là x và toa độ imaginary là y.
Việc tính tổng các số phức đơn giản chỉ việc tình các toán độ
Real-part(z1 + z2) = Real-part(z1) + Real-part(z2),
Imaginary-part(z1 + z2) = Imaginary-part(z1) + Imaginary-part(z2).
Khi nhân các số phức, tự nhiên để nghĩ trong các điều khoản về việc trình bày một số phức trong form polar, như là một magnitude và một angle(r và A trong hình 2.2). Kết quả phép nhân hai số phức là một vector đạt được bởi sự co giản một số phức bởi độ dài của một số phức khác và sau đó xoay nó thông qua một gốc khác.
Magnitude(z1 · z2) = Magnitude(z1) · Magnitude(z2),
Angle(z1 · z2) = Angle(z1) + Angle(z2).
Hơn nữa, có hai cách để trình bày các số phức, tương ứng với các phép tính toán khác nhau. Vâng đúng thế, từ quan điểm của một người viết chương trình sử dụng các số phức, nguyên tác của data abstraction chỉ ra rằng tát cả các toán tử thao tác với số phức nên có giá trị bất kể cách trình bày nào cho số phức được sử dụng trong máy tính. Ví dụ, chúng thường hữu dụng để tìm magnitude của một số phức cụ thể bởi các tọa độ của hình chữ nhật. Đơn giản, chúng thường có thể quyết định phần thực của một số phức tương ứng bởi tọa độ polar.
Để thiết kế như một hệ thống, chúng ta có thể làm theo chiến lược tương tự như với data abstraction chúng ta đã được làm trong việc thiết kế package của phân số trong các bài trước. Cho rằng các toán tử của số phức được thực thi trong điều khoản của selectors sau: real-part, imag-part, magnitude và angle. Cũng như cho rằng chúng ta có hai procedure cho việc khởi tạo các số phức: make-from-real-imag trả về một số phức với các phần thực và phần ảo cụ thể, và make-from-mag-ang trả về một số phức với magnitude và angle cụ thể. Các procedure này có các thuộc tính như sau đối vơi bấy kì số phức nào.
(make-from-real-imag (real-part z) (imag-part z))
và
(make-from-mag-ang (magnitude z) (angle z))
Tạo các số phức bằng z.
Sử dụng constructor và selector, chúng ta có thể thực thi đại số trên các số phức sử dụng “abstract data” cụ thể bởi constructor và selector, như chúng ta đã làm với phân số trong bài trước. Như đã đưa ra công thức ở trên, chúng ta có thể cộng và trừ các số phức trong các điều khoản của phần thực và ảo trong khi nhân và chia các số phức trong các điều khoản của magnitude và angle.
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
Để hoàn thành package của số phức, chúng ta phải chọn một sự trình bày và chúng ta phải thực thi constructors và selectore tron các điều khoản của các số nguyên thủy và cáu trúc list nguyên thủy. Có hai cách để làm điều đó: Chúng ta có thể trình bày một số phức trong ” retangular form” như là một pair( phần thực và phần ảo) hoặc trong “polar form” như là pair (magnitude, angle). Chúng ta sẽ chọn cách thức nào?
Để khởi tạo cho các lựa chọn khác, tưởng tượng có hai lập trình viên, Ben Bitdidle và Alyssa P.Hacker, người độc lập trong việc trình bày các thiết kế cho hệ thống số phức. Ben chọn trình bày các số phức trong retangular form. Với lựa chọn này, chọn phần thực và ảo của một số phức là dễ dàng, như là việc khởi tạo một số phức với các phần thực và phần ảo cho trước. Để tìm magnitude và angle, hoăc để khởi tạo một số phức với một magnitude và angle cho trước, anh ta sử dụng mối quan hệ lượng giác.
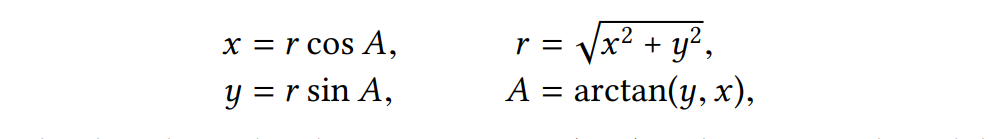
nó thể hiện sự liên quan đến phần thực và ảo (x, y) đến magnitude và angle (r, A). Vì vậy sự trình bày được cho bởi selector và constructor như sau:
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (magnitude z)
(sqrt (+ (square (real-part z))
(square (imag-part z)))))
(define (angle z)
(atan (imag-part z) (real-part z)))
(define (make-from-real-imag x y) (cons x y))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a))))Alyssa thì ngược lại, chọn trình bày các số phức trong polar form. Việc chọn magnitude và angle là dễ dàng, nhưng cô ấy phải sử dụng mối quan hệ lượng giác để đạt được phần thực và ảo . Trình bày như sau:
(define (real-part z) (* (magnitude z) (cos (angle z))))
(define (imag-part z) (* (magnitude z) (sin (angle z))))
(define (magnitude z) (car z))
(define (angle z) (cdr z))
(define (make-from-real-imag x y)
(cons (sqrt (+ (square x) (square y)))
(atan y x)))
(define (make-from-mag-ang r a) (cons r a))