Như là một minh chứng cho việc thao tác biểu tượng và hơn thế nữa của data abstraction, để thiết kế một procedure trình diễn các biểu thức đại số khác nhau của các biểu tượng. Chúng ta tạo procedure cần các đối số là các biểu thức đại số và một biến và trả về giá trị đạo hàm của biểu thức . Ví dụ, nếu đối số của một procedure là ax^2 +bx + c và x thì procedure nên trả về 2ax +b. Sự khác biệc của việc thao tác với symbols chính là sự cụ thể lịch sử của Lisp. Nó là một trong những ví dụ ấn tượng đằng sau sự phát triển của ngôn ngữ máy tính cho việc thao tác với symbol. Hơn nữa, nó đánh dấu sự bắt đầu của dòng sự kiên nghiên cứu dẫn chúng ta đến đi lên của các hệ thống mạnh mẽ khi làm việc với symbol, chúng đang được sử dụng bởi sự phức tạp hơn của số trong toán học và vật lý.
Trong sự phát triển của chương trình với sự khác biệt của symbol, chúng ta sẽ follow cùng chiến lược của data abstraction mà chúng ta đẫ follow để tạo ra hệ thống phân số. Đầu tiên, chúng ta sẽ định nghĩa một thuật toán khác biệt tính toán trên các abstract object như là “sums,” “products,” và “variables” không cần quan tâm về cách chúng được trình bày. Sau đó chúng ta sẽ đưa ra vấn đề.
The differentiation program with abstract data
Để cho mọi thứ đơn giản, chúng ta cùng xem một chương trình symbol cực đơn giản nó xử dụng các biểu thức tính toán của add và mul và không có parameter. Sự khác biệt của bất kỳ biểu thức có thể được tiến hành bằng cách áp dụng các nguyên tắc giảm dần sau đây:
dc/dx = 0, với c là một hằng số hoặc một biến khác x
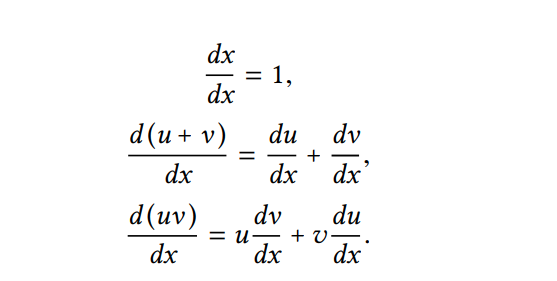
Hãy quan sát xem hai quy tắc sau là đệ quy tự nhiên, đó là để đạt được đạo hàm của một sum chúng ta tìm đạo hạm của các điều khoản và add chúng với nhau. Mỗi điều kiệp đáp ứng có thể là một biểu thức cần được bốc tách riêng biệt. Việc bóc tách ra thành các mẫu nhỏ hơn thậm chí có thể tạo ra nhiều mẫu nhỏ hơn nữa có thẻ là hằng số hoặc các biến, đạo hàm có lẽ là 0 hoặc 1.
Để tận dụng các quy tắc này trong một procedure, chúng ta cần xem xét một ích tính suy nghĩ cẩn thận, như chúng ta đã làm trong việc thực thi phân số. Nếu chúng ta có một sự hiểu biết cho việc trình bày các biểu thức đại số, chúng ta nên xem biểu thức đó là sum, product, constant hay một biến. Chúng ta nên truy xuất các phần của một biểu thức. Ví dụ, đối với biểu thức sum, chúng ta muốn truy xuất addend ( điều khoản đầu tiên) và augend (thứ hai). Cho rằng chúng ta đã có các procedure để thực thi việc chọn, khởi tạo và predict.
(variable? e) e có phải là một biến hay không?
(same-variable? v1 v2) v1 và v2 có tương đương nhau hay không?
(sum? e) e là một sum ?
(addend e) addend của một sum e.
(augend e) augend của một sum e.
(make-sum a1 a2) khởi tạo sum của a1 và a2.
(product? e) e là một procduct?
(multiplier e) multiplier của product e.
(multiplicand e) Multiplicand của product e.
(make-product m1 m2) khởi tạo product của m1 và m2.
Sử dụng các khái niệm trên và predicate nguyên thủy number?, nó xác định các số, chúng ta có thể trình bày các quy tắc khác biệt như là procedure sau:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp) (if (same-variable? exp var) 1 0))
((sum? exp) (make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type: DERIV" exp))))procedure deriv kết hợp với thuật toán vi phân tạo ra các kiều khoản của data abstract, nó sẽ hoạt động không cần phải quan tâm cách chúng ta trình bày các biểu thức đại số, miễn là chúng ta thiết kế một set của hàm khởi tạo và truy xuất phần tử tương ứng. Đây sẽ là một vấn đề chúng ta phải quan tâm trong bài tiếp theo.



